Georeferencing and coordinate systems

Georeferencing is about using map coordinates to assign a spatial location to map features. All the elements in a map layer have a specific geographic location and extent that enables them to be located on or near the earth's surface. The ability to accurately locate geographic features is critical in both mapping and GIS.

Describing the correct location and shape of features requires a coordinate framework for defining real-world locations. A geographic coordinate system is used to assign geographic locations to objects. A global coordinate system of latitude-longitude is one such framework. Another is a planar or Cartesian coordinate system derived from the global framework.

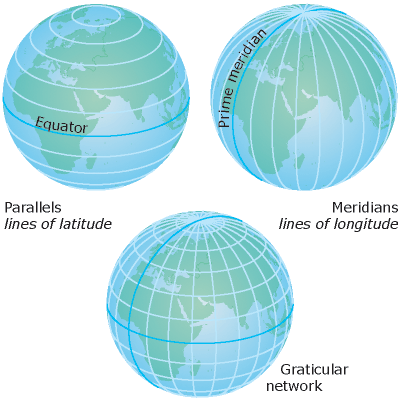
Maps represent locations on the earth's surface using grids, graticules, and tic marks labeled with various ground locations—both in measures of latitude-longitude and in projected coordinate systems such as UTM meters. The geographic elements contained in various map layers are drawn in a specific order (one on top of another) for the given map extent.

GIS datasets contain coordinate locations within a global or Cartesian coordinate system to record geographic locations and shapes. In this way, multiple GIS data layers can be overlaid onto the earth's surface.

Latitude and longitude

One method for describing the position of a geographic location on the earth's surface is using spherical measures of latitude and longitude. They are measures of the angles (in degrees) from the center of the earth to a point on the earth's surface. This type of coordinate reference system is often referred to as a geographic coordinate system.

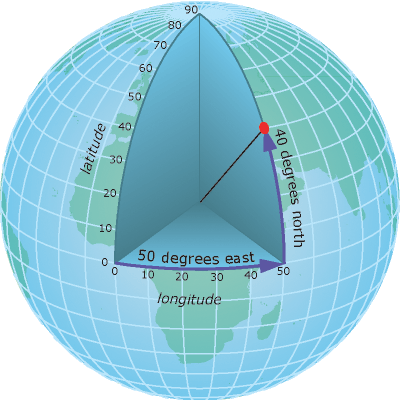
Longitude measures angles in an east–west direction. Longitude measures are traditionally based on the prime meridian, which is an imaginary line running from the North Pole through Greenwich, England, to the South Pole. This angle is longitude 0. West of the prime meridian is typically recorded as negative longitude, and east is recorded as positive. For example, the location of Los Angeles, California, is roughly plus 33 degrees, 56 minutes latitude and minus 118 degrees, 24 minutes longitude.

Although longitude and latitude can locate exact positions on the surface of the globe, they do not provide uniform units of measure for length and distance. Only along the equator does the distance represented by one degree of longitude approximate the distance represented by one degree of latitude. This is because the equator is the only parallel as large as a meridian. (Circles with the same radius as the spherical earth are called great circles. The equator and all meridians are great circles.)

Above and below the equator, the circles defining the parallels of latitude get gradually smaller until they become a single point at the North and South Poles where the meridians converge. As the meridians converge toward the poles, the distance represented by one degree of longitude decreases to zero. On the Clarke 1866 spheroid, one degree of longitude at the equator equals 111.321 kilometers, while at 60° latitude, it is only 55.802 kilometers. Since degrees of latitude and longitude don't have a standard length, you can't measure distances or areas accurately or display the data easily on a flat map or computer screen. Using many (but not all) GIS analysis and mapping applications often requires a more stable, planar coordinate framework, which is provided by projected coordinate systems. Alternatively, some of the algorithms used for spatial operators take into account the geometric behavior of spherical (geographic) coordinate systems.

Map projections using Cartesian coordinates

A projected coordinate system is any coordinate system designed for a flat surface, such as a printed map or a computer screen.

Both 2D and 3D Cartesian coordinate systems provide the mechanism for describing the geographic location and shape of features using x- and y-values (and as you will read later, by using columns and rows in rasters).

The Cartesian coordinate system uses two axes: one horizontal (x), representing east–west, and one vertical (y), representing north–south. The point at which the axes intersect is called the origin. Locations of geographic objects are defined relative to the origin, using the notation (x,y), where x refers to the distance along the horizontal axis and y refers to the distance along the vertical axis. The origin is defined as (0,0).

In the illustration below, the notation (4,3) records a point that is four units over in x and three units up in y from the origin.

3D coordinate systems

Increasingly, projected coordinate systems also use a z-value to measure elevation above or below mean sea level.

In the illustration below, the notation (2,3,4) records a point that is two units over in x and three units in y from the origin and whose elevation is four units above the earth's surface (such as 4 meters above mean sea level).

Properties and distortion in map projections

Since the earth is spherical, a challenge faced by cartographers and GIS professionals is how to represent the real world using a flat or planar coordinate system. To understand the dilemma, consider how you would flatten half of a basketball; it can't be done without distorting its shape or creating areas of discontinuity. The process of flattening the earth is called projection, hence the term map projection.

A projected coordinate system is defined on a flat, two-dimensional surface. Projected coordinates can be defined for 2D (x,y) or 3D (x,y,z) in which the x,y measurements represent the location on the earth's surface and z would represent height above or below mean sea level.

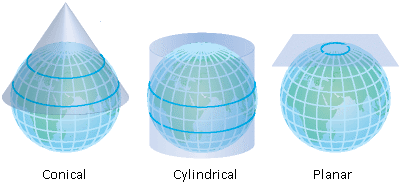
Unlike a geographic coordinate system, a projected coordinate system has constant lengths, angles, and areas across the two dimensions. However, all map projections representing the earth's surface as a flat map create distortions in some aspect of distance, area, shape, or direction.

Users cope with these limitations by using map projections that fit their intended uses, their specific geographic location, and extent. GIS software also can transform information between coordinate systems to support integration of datasets held in differing coordinate systems and to support a number of critical workflows.

Many map projections are designed for specific purposes. One map projection might be used for preserving shape while another might be used for preserving the area (conformal versus equal-area projections).

These properties—the map projection along with spheroid and datum—become important parameters in the definition of the coordinate system for each GIS dataset and each map. By recording detailed descriptions of these properties for each GIS dataset, computers can reproject and transform the geographic locations of dataset elements on the fly into any appropriate coordinate system. As a result, it's possible to integrate and combine information from multiple GIS layers regardless of their coordinate systems. This is a fundamental GIS capability. Accurate location forms the basis for almost all GIS operations.